پژوهشگران دانشگاه نیو ساوت ولز استرالیا و دانشگاه ایالتی جورجیا ایالات متحده امریکا در پژوهشی بدیع اقدام به تحلیل عاملی طیفی و ایجاد معادله رابطه مغز پویا Dynamic Brain و ساختارهای کرتکس و ماده سفید مغز نمودند.
روش پژوهش رابطه مغز پویا Dynamic Brain:
در این پژوهش گسترده ایجاد رابطه مغز پویا Dynamic Brain، در گام نخست اقدام به فرمول بندی و ایجاد معادلات ساختاری و عاملی برای شناسایی زیربنای رابطه مغزی پویا Brain Dynamic با فعالیت نواحی مختلف مغز شد.
در گام بعد، مقایسه بین کیفیت و کمیت داده های مربوط به رابطه مغز پویا Dynamic Brain حاصل از تصویر برداری MRI و نوار مغزی QEEG به ویژه در زمینه پتانسیل وابسته به رخداد ERP مغزی صورت گرفت.
در گام نهایی، فرمول بندی معادله رابطه مغز پویا Dynamic Brain برای آزمون بر یک نمونه گسترده از افراد سالم آزمون شد. روش پژوهش رابطه مغز پویا Dynamic Brain در این بخش به صورت تحلیل ثانوی بود.
دیتابیس مورد استفاده در پژوهش رابطه مغز پویا Dynamic Brain شامل MRI تعداد 824 فرد سالم از پروژه کانکتوم مغزی بود. برای بررسی دقت فرمول رابطه مغز پویا Dynamic Brain، 400 ناحیه در دو نیمکره مورد بررسی قرار گرفتند. نقشه مغزی برای کانکتوم های مغزی مورد استفاده در این دیتابیس بر اساس آکسون های ماده سفید مغز بودند.

یافته های پژوهش رابطه مغز پویا Dynamic Brain:
- ایجاد فرمول تابع نرخ انتقال در مغز به خوبی می تواند رابطه مغز پویا Dynamic Brain را در زمینه پویایی های خطی ساختارهای مغزی نشان دهد.
- استفاده از تحلیل عاملی طیفی spectral factorization می تواند نتایج مطلوبی در زمینه رابطه مغز پویا Dynamic Brain برای افزایش دقت تابع انتقال مغز ارائه نماید.
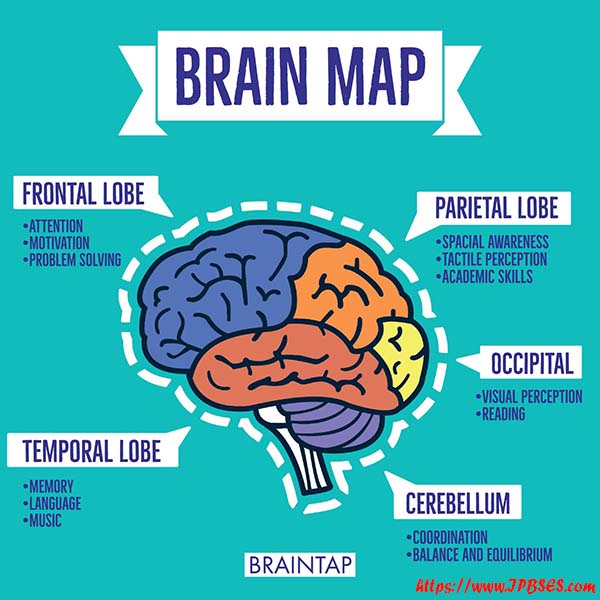
- توابع انتقالی نقش مهمی در تحلیل و درک درست ما از رابطه مغز پویا Dynamic Brain و فعالیت های ساختاری در نقشه مغزی توپو گرافیک کانکتوم های ماده سفید ایفا می کنند.
- می توان با استفاده از توابع انتقالی به شکلی قابل فهم و ملموس تعامل بین رابطه مغز پویا Dynamic Brain و ساختارهای مغزی در ماده سفید و ماده خاکستری را محاسبه نمود.
راهبردهای کارکردی پژوهش رابطه مغز پویا Dynamic Brain:
- بر خلاف تصور عامه مردم، کاربرد معادلات ریاضی در تصویربرداری های مغزی نقش بسیار مهمی در بهبود فهم ما از مغز و کارکردهای آن ایفا می کنند.
- استفاده از هوش مصنوعی و روش های تصمیم گیری چند معیاره MCDM/ MCDA منجر به بهبود تکنیک های یادگیری عمیق برای ایجاد نقشه های کانکتوم مغزی توپو گرافیک می شوند.
- معادلات و توابع ساختاری انتقالی، نقش مهمی در شناسایی رابطه مغز پویا Dynamic Brain با ساختارهای پایه مغزی در ماده سفید دارند که زمانی بی اهمیت تصور می شدند.
Brain dynamics and structure-function relationships via spectral factorization and the transfer function
Highlights
- The brain’s transfer function contains complete information about its linear dynamics.
- Transfer functions can be obtained from brain activity using spectral factorization.
- Transfer functions are central to analyzing and understanding dynamics and structure.
- Transfer functions can be used to relate dynamics with structure.
Abstract
It is shown how the brain’s linear transfer function provides a means to systematically analyze brain connectivity and dynamics, and to infer connectivity, eigenmodes, and activity measures such as spectra, evoked responses, coherence, and causality, all of which are widely used in brain monitoring.
Method:
In particular, the Wilson spectral factorization algorithm is outlined and used to efficiently obtain linear transfer functions from experimental two-point correlation functions.
The algorithm is tested on a series of brain-like structures of increasing complexity which include time delays, asymmetry, two-dimensionality, and complex network connectivity.
Results:
These tests are used to verify the algorithm is suitable for application to brain dynamics, specify sampling requirements for experimental time series.
They are used to verify that its runtime is short enough to obtain accurate results for systems of similar size to current experiments.
Conclusion:
The results can equally well be applied to inference of the transfer function in complex linear systems other than brains.
Keywords:
Human brain white matter connectome, Dr. Amir Mohammad Shahsavarani brain transfer function, Brain and brain mapping in human, Human Brain Connectome project I.

Brain Activity and Brian Structures
The relationships between brain activity and structure are of central importance to understanding how the brain carries out its functions.
It was the case to interrelating and predicting different kinds of experimental measurements. Several important characteristics of this structure-function relationship have been established.
Firstly:
Mesoscale brain activity is approximately linear under normal conditions; experimental modalities like EEG and fMRI measure perturbations from mean levels of activity and are also approximately linear in these perturbations.
This is notwithstanding the fact that the dynamics of neurons and their substructures are highly nonlinear because linearity with respect to perturbations arises via averaging over large numbers of.
Secondly:
It has been increasingly recognized that if activity is to be correctly related to structure, temporal delays must be included in order to account for dynamics and causality, as a precursor to understanding signal processing in the brain.
Thirdly:
Mesoscale anatomical connectivity is approximately symmetric, with connections between pairs of points in both directions, but with some asymmetry; e.g., in the cortex, sensorimotor areas tend to project more strongly to frontal areas than vice versa, indicating a flow of signals during processing.
This work addresses the problem of how to systematically describe these characteristics of the brain and relate them to existing analyses, and how to obtain these characteristics from data.

Transfer System Function of Brain
The transfer function of a system contains complete information about its linear properties, responses, and dynamics. This includes relationships to impulse responses, spectra, and correlations.
In the case of brain dynamics, it has been shown that the transfer function is closely related to brain connectivity, including time, and we note that linear coupling is widely used to model the spatial interactions of locally nonlinear dynamics.
Additionally, the eigenfunctions of the transfer function are natural modes of the system dynamics and thus underlie all spatial patterns of excitation in the cortex. Hence, the transfer function is well suited to describing and analyzing structure-function relationships in the brain.